ヒープソートのスワップ回数のワーストケースの生成: アルゴリズムとデータ構造入門
この記事について
Aizu Online Judgeに掲載されている問題をC++(大体C++11)で解くという遊びをしているので、考え方の例と解けたコード例を記録していこうかと思います。コード例はたたんでおきます。クリックやタップでコード例を開けます。
こちらの問題:
今回は難しかった…
ALDS1_9_D: Heap Sort: ヒープソート
ヒープソートという題にも関わらず、別にヒープソートを実装するわけではないだろうなということには問題文からすぐ気付きました。
出力すべきものは、最初のヒープ構築時を除いて、ヒープソートを行っている間に実行した要素の交換回数が最悪になる場合の順列です。
一体どんな順序で並べればワーストケースになるのか…と結構途方にくれました。
ごく単純な考え
真っ先に思いつき、かつ、まあ無理だろうと思ったのは、全ての順列でヒープソートを行い、実際に交換回数を数えていく、という方法でした。$n!\ (1 \le n \le 200,000)$じゃん…何時間かかるんだ、となりました。
最悪交換回数を事前に求めたとしても全順列のどのあたりに来るのかわからないので難しいと思います。
そのためまずはヒープソートでしていることを考えてみたいという流れになりました。
特徴を考える
ヒープソート自体は、その配列の中で、
- 最大ヒープ(
max heap)を構築する - 最大値(ヒープの先頭)をヒープ内の最後尾と交換してヒープサイズをデクリメントする
のようにし、手順2を繰り返して、大きい順に後ろから並べていくことでソートが達成できるという仕組み。(あとでもう少し細かく見ます)
手順2で交換した後、ヒープが崩れて再構築する必要があり、ここでの要素交換の回数の総数が最大になって欲しいのです。
ヒープの構築・再構築は、次の関数で実行できます(ほぼ問題文の擬似コード通り):
// C++
void maxHeapify(std::vector<int> *A, int i, int heapsize)
{
int l = i * 2;
int r = i * 2 + 1;
int largest = 0;
if (l <= heapsize && ((*A)[l] > (*A)[i]))
largest = l;
else
largest = i;
if (r <= heapsize && ((*A)[r] > (*A)[largest]))
largest = r;
if (largest != i)
{
std::swap((*A)[i], (*A)[largest]);
// 交換回数の記録
(*A)[0]++;
// ダウンヒープ
maxHeapify(A, largest, heapsize);
}
}配列AはN+1の要素数を持ち、添字1をヒープ全体の根として扱います。A[0]は使わないので、交換回数の記録用に使っています。
heapsizeは配列内でヒープとみなしている範囲の終端のインデックスです。A[heapsize+1]以降はソート済みということを意味します。
最大2個の子のうちで大きいものを持ち上げ、値の小さいノードをだんだんと下へ押し下げていきます(ダウンヒープ)。1回押し下げるたびに交換回数が1増えます。
ノードが子より既に大きい場合は何もしません。(この点が重要です。)
実際ではこの関数は使わなくても済みました。また、問題文のサンプル入力のような要素が8個くらいの小さい配列で色々見ていると分かってくることがあります。
- ソート中にヒープを再構築するとき、ダウンヒープが葉まで到達しないとワーストケースにならない。
- ワーストケースの交換回数は要素数から求められそうだ。
- 解答はヒープ条件を満たしたものが求めやすそうだ。
ということを考えました。2に関しては、交換回数を求めてもあまり使う用途がなさそうです。1は使えそうだなあとは思いました。3については、解答になる順列は、ヒープ条件を満たしたものの方が考えやすそうだなという感じはしました。
このようなことを考えはしたもののまだ実際の方針には靄がかかっていました。
ちょっとネットで調べた
heapsort worstcaseなどで検索して見ることにしました。すると、結構昔の論文が当たりました。A WORST CASE ANALYSIS OF HEAPSORTというそのままなタイトルでした。リンクは下部の参考に張っておきます(PDF)。
これはヒープ再構築時の比較回数が最悪になるケースの研究のようです。また、完全2分木を前提にしていました。
ちょっと読むのに苦労した後、ヒープソートの逆を行えば作れる、ということだと思いました。
逆を考える
ヒープソートの逆を考えてみます。ヒープソートでは特徴を考えるで考えた通り、構築されたヒープで交換と再構築を繰り返します。具体的には、
- 配列を最大ヒープの構造で用意する
- ヒープサイズをNとする
- ヒープサイズが1より大きい限り以下を繰り返す
- 先頭ノードとヒープの終端ノードを交換する
- ヒープサイズをデクリメントする
- 先頭ノードをダウンヒープする
- (配列が昇順でソートされる)
を行います。これの逆は、
- 配列を昇順でソートしたものを用意する
- ヒープサイズを1とする
- ヒープサイズがNより小さい限り以下を繰り返す
- ヒープの終端ノードをアップヒープする
- ヒープサイズをインクリメントする
- 先頭ノードとヒープの終端ノードを交換する
- (配列が最大ヒープの構造になるはず)
を行うことです。初めにソートしておくのは、ヒープソートの逆を行うためです。これにより、ヒープ領域には小さい値から順に加わっていくことになります。
ループ中に行うアップヒープでは必ずヒープの中の最小値のノードが選ばれて根へ運ばれます。ヒープサイズがインクリメントされた後は、最大値のノードがヒープの終端に現れますが、先頭と交換されることで、最大値のノードは根になり、最小値のノードはヒープ終端へ移ります。そのためループの先頭で行うアップヒープは必ず最小値のノードが選ばれます。(ソート済みのため1回目のループでも同じになります。)
アップヒープですることは、対象の値のノードと親ノードとの交換を繰り返して先頭ノードまで引き上げることです。ヒープソートでのダウンヒープでは最大ヒープ条件を満たすかどうかのチェックをしていましたが、逆操作でのアップヒープでは何もチェックせずに根まで交換し続けます(ヒープには要素が昇順に追加されていくので最大ヒープが崩れることはありません)。全体を通してこうすることで、ヒープソートで行うダウンヒープでは必ず葉まで押し下げられることになります。
アップヒープと言いながら、ヒープ条件を満たしつつ動かすわけではないので、本当は違う名称がいいです。参考の研究に倣い、unsiftと以降は呼称します。
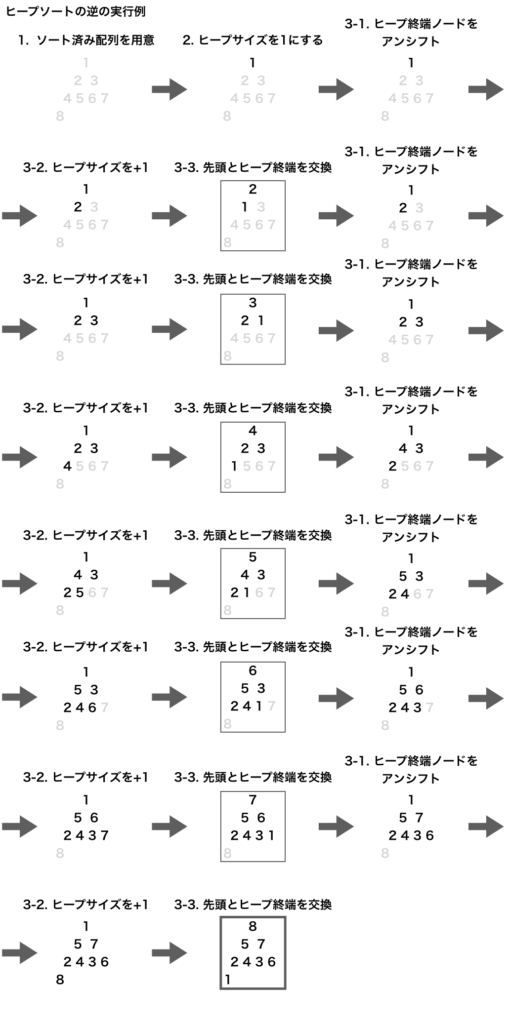
ヒープソートの逆を具体例で考えてみます。1から8の整数8個で考えます。同じ値は必ず存在しないので、大小関係の定まった8個の整数すべてで同じことが成り立ちます。
見出しの番号は、上のヒープソートの逆の手順と対応させています。 1回ループが終わった状態のものには枠線をつけています。最終的なヒープは太めの枠線にしています。
逆の操作なので当たり前ですが、最後の方から逆向きにたどれば、ヒープソートになります。 そしてそのとき、必ず葉まで押し下げられるということは、ワーストケースになるということになるので、問題を解決することができます。
あとはこれを実装すれば終わりです。
コード例
実装は逆にするだけだったのでスムーズにできました。ヒープソートの逆操作のループでは、for文を使ったので、若干の読み替えが必要な点はご留意ください。
unsiftにあまり用途がないbound引数があるのは参考研究を参考した名残です。
折り畳んであります。
// Heap Sort
#include <iostream>
#include <vector>
#include <algorithm>
void unsift(std::vector<int> *A, int i, int bound);
void reverseSorting(std::vector<int> *A);
int main()
{
int N;
std::cin >> N;
std::vector<int> A(N + 1, 0);
for (size_t i = 0; i < N; i++)
{
int a;
std::cin >> a;
A[i + 1] = a;
}
reverseSorting(&A);
for (size_t i = 0; i < N; i++)
{
if (i != 0)
std::cout << " ";
std::cout << A[i + 1];
}
std::cout << std::endl;
return 0;
}
// 今回の用途ではboundは1で固定なので引数としては本当は無用
void unsift(std::vector<int> *A, int i, int bound)
{
int parent = i / 2;
if (parent >= bound)
{
// std::cout << " swap: " << (*A)[i] << "<->" << (*A)[parent] << std::endl;
// 無条件で交換していく
std::swap((*A)[i], (*A)[parent]);
unsift(A, parent, bound);
}
}
void reverseSorting(std::vector<int> *A)
{
std::sort(A->begin() + 1, A->end());
int N = A->size() - 1;
// iをヒープ領域の終端とする
for (size_t i = 1; i < N; i++)
{
// 常にヒープの最後尾が最小値
// ヒープ範囲内の最小値を先頭へアンシフトする
unsift(A, i, 1);
// 先頭に来た最小値とヒープの最後尾の1つ後ろを交換
std::swap((*A)[1], (*A)[i + 1]);
}
}こまごまとしたこと
以降は、解く上ではあまり関係ないけれど、思ったことなどを書いておきます。
ワーストケースの交換回数
解くうえでは使いませんでしたが、ワーストケースにおけるヒープ再構築のためのスワップ回数を一応求めておいたので残しておきます。間違っている可能性もありますのでご留意ください。
まずは用語を2つ定義しておきます(枝、レベルの2つ)。根、葉、ノードなどはだいたい共通の認識であると思うので省略します。枝はノードとノードを接続する辺です。 ある葉ノードから根ノードまでにたどる枝の最小本数をレベルと呼ぶことにします。根ノードのレベルは $0$ とします。
ある木構造 $T$ のノード数を $n$ とするとき、レベルの最大値 $l_{max}$ は、 $l_{max} := \lfloor \log{n} \rfloor$ になります。logの底は $2$ です。
ヒープサイズが $i$ のときに再構築を行うとすると、根からダウンヒープが始まりますが、ワーストケースになるためには、ダウンヒープがその時点での最も大きいレベルまで行われる必要があります。
このときのレベルの最大値は $l := \lfloor \log{i} \rfloor$ であり、そのレベルにあるノードの分だけヒープの再構築が行われます。そのため、 $l_{max}$ とそれ以外におけるレベルでは、ヒープの再構築回数が異なると思われます。レベルごとのダウンヒープを行うノードの個数は、レベル $l_{max}$ 以外では $2^l$ 個、レベル $l_{max}$ では、完全2分木とは限らなくて、ヒープの再構築前にヒープサイズをデクリメントするので、 $n-2^{l_{max}}$ 個というふうになります。
それぞれの場合の葉までのダウンヒープ回数はそのレベルと一致、つまり $l$ 回になり、レベル $0$ ではヒープサイズが $1$ になり何もしないので、最大交換回数 $SC$ は、
$$ \begin{align*} SC &= \sum_{l=1}^{l_{max}-1} {(l\cdot 2^l)} + (N-2^{l_{max}}) \cdot l_{max} \\ &= (l_{max}-2)\cdot 2^{l_{max}} + 2 + (N-2^{l_{max}}) \cdot l_{max} \\ &= N\cdot l_{max} - 2^{l_{max}+1} + 2 \end{align*} $$
になります。
すべての順列の列挙するコード例
サイズ8の配列については、すべての順列を出力してみたりはしてました。C++では、std::next_permutation()を使用すると便利です。降順の方にワーストケースが集中しているんじゃないかと思い、コード例ではstd::prev_permutation()を使っています。イテレータからイテレータまでの間の要素を順列として捉えて、直前または直後になる順列に並び替えてくれます。
Pythonでもitertools.permutations()が使えます。
// a permutation example
#include <iostream>
#include <vector>
#include <algorithm>
void maxHeapify(std::vector<int> *A, int i, int heapsize);
void heapSort(std::vector<int> *A);
void print(std::vector<int> *A)
{
for (auto &&i : *A)
{
std::cout << i << " ";
}
std::cout << std::endl;
}
int main()
{
const int N = 8;
std::vector<int> A(N + 1, 0);
for (size_t i = N; i > 0; i--)
{
A[N - i + 1] = i;
}
// 最初のも処理するためdo-whileで回す
do
{
// もとのAの並びを変えないためコピーを並び替える
std::vector<int> cpA(A);
heapSort(&cpA);
// 交換回数と元の順列を表示
A[0] = cpA[0];
print(&A)
} while (std::prev_permutation(A.begin() + 1, A.end()));
return 0;
}
void maxHeapify(std::vector<int> *A, int i, int heapsize)
{
int l = i * 2;
int r = i * 2 + 1;
int largest = 0;
if (l <= heapsize && ((*A)[l] > (*A)[i]))
largest = l;
else
largest = i;
if (r <= heapsize && ((*A)[r] > (*A)[largest]))
largest = r;
if (largest != i)
{
std::swap((*A)[i], (*A)[largest]);
// 交換回数の記録
(*A)[0]++;
maxHeapify(A, largest, heapsize);
}
}
void heapSort(std::vector<int> *A)
{
// build max heap
auto N = A->size() - 1;
for (size_t i = N / 2; i > 0; i--)
{
maxHeapify(A, i, N / 2);
}
(*A)[0] = 0;
// sorting
int heapsize = N;
while (heapsize > 1)
{
std::swap((*A)[1], (*A)[heapsize]);
heapsize--;
maxHeapify(A, 1, heapsize);
}
}mathjaxで行揃え・行番号の調整
latexの記法で記事が書けるmathjaxを使っています。この記事にも使っていて、記法などを調べることがあるので、メモを残しておきたくここに書いておきます。
=などで揃えたいときはalignが使えます。揃えたいところの前に&をつけると揃えられます。
後ろに*をつけることで行番号を非表示にできます。latexでは\\で改行できたと思いますが、markdownで書いている場合は、エスケープする必要があるので、\\\\が必要です。
$$ \begin{align*}
S &= 1 + 2 + 3 \\\\
&= 6 \\\\
\end{align*}
$$のようにmarkdownで書くと、
$$ \begin{align*} S &= 1 + 2 + 3 \\ &= 6 \\ \end{align*} $$
となります。
参考
- A WORST CASE ANALYSIS OF HEAPSORT (PDF形式です)
- next_permutation - cpprefjp C++日本語リファレンス
- Pythonでの順列操作
おわり
ワーストケースの考慮は大事ですね。スワップ回数に注目することもあるんだなと感心しました。分かりきったことですが、連結リストとかではヒープソートが使い物にならないことも想像に易くなります。
逆を考えるという発想には成る程なるほどと唸りました。参考にした研究のPDFファイルが割と肝心なところで落丁しているようでちょっと残念でしたが、付録の方に完全な擬似コードがあって助かりました。
以上です。




コメント