二分探索で範囲の端を探す

二分探索を少し深める

二分探索の基本
応用
応用の単純な例
使ったところ
おわり

二分探索の基本

二分探索といえばソート済みの配列などから目的のものを見つけ出すアルゴリズムのひとつ。

大まかなアルゴリズムは次の通り:

ソート済みの配列などを用意する。
両端を決める。
両端に対する中央を決める。
中央が目的の値かそうでないか調べる。目的値なら終了。
3でそうでないなら、中央と目的値の順序関係に応じて、両端のいずれかを更新し、2に戻る。

というアルゴリズムをまず学ぶものだと思う。探索範囲の二分を繰り返していくので配列のサイズをnとすれば、$O(\log{n})$の計算量になる。

応用

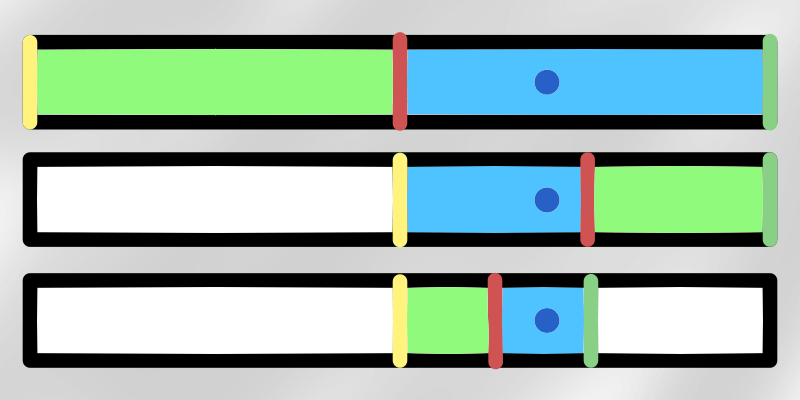
目的の値の判定部分に注目すれば、$=$か$\gt$か$\lt$の3択になっていることが分かる。これは、$\geq$か$\lt$、もしくは$\leq$か$\gt$の2択でもいいようだ。

どういうことかといえば、最大値の最小値や、最小値の最大値を求めるのにも使えるということ。もっと言い換えれば、条件（不等式）を満たすものの左端もしくは、右端を求めるために使えるということ。

大まかなアルゴリズムは以下の通り（最大値の最小値つまり左端を見つける場合）:

ソート済みの配列などを用意する。
両端を決める。
両端のインデックスの差が1以下ならば、繰り返し終了。右側の端が目的値のインデックスとなる。
両端に対する中央を決める。
中央の値が条件を満たしているか判定する。
条件を満たしているなら、左側に条件を満たすものがあるかもしれないので、左半分について、1に戻る。
条件を満たさないなら、右側に条件を満たす範囲の左端があるので、右半分について、1に戻る。

応用の単純な例

最大値の最小値を求める例を単純な例で実装した。若干わかりづらいが、添字と値が一致していると考えて、配列は用意せずに、[0, N)の整数を探索している。もし値が別にあるなら、配列などを用意して、値計算作業は省略のところで何か必要なことをする。

最初はl=-1でないとダメなことに今更気づいた。1回はwhileの中を通す必要がある。

C++とPython3で書いた。まずはC++から。

// 二分探索の確認

#include <iostream>

int main()
{
    // 0からNまでの整数の間で探索する。
    // この例では、添字だけを考えているので、配列はない。
    const int N = 1e5;
    // 適当に10個ほど探す例
    for (int i = 1e5 - 10; i < N; i++)
    {
        // ここからがメイン。
        // iを見つけたい値とする
        std::cout << " target: " << i << std::endl;
        int l = -1, r = N;
        int c = l + (r - l) / 2;
        while (r - l > 1)
        {
            // 値計算作業は省略
            if (c >= i)
            {
                // まだ左へ行ける
                r = c;
                c = l + (r - l) / 2;
            }
            else
            {
                l = c;
                c = l + (r - l) / 2;
            }
            std::cout << "  next info: l: " << l << " c: " << c << " r: " << r << " i: " << i << std::endl;
        }
        // iとrは一致しているはず。
        std::cout << "i: " << i << " was found! the index: " << r << std::endl;
    }
    return 0;
}

Python3でも書いた。だいたい同じ。違いはチェックにassertを使ったくらい。

"""二分探索の例"""

if __name__ == "__main__":
    N = int(1e5)
    # 出力を控えたので、全ての添字を見つけようとしてみる。
    for i in range(0, N):
        l = -1
        r = N
        c = l + (r - l) // 2
        while r - l > 1:
            # 値の計算作業は省略
            if (c >= i):
                # 左へ
                r = c
                c = l + (r - l) // 2
            else:
                # 右へ
                l = c
                c = l + (r - l) // 2
            # print(f'  next info: l: {l} c: {c} r: {r} i: {i}')
        try:
            assert i == r
        except AssertionError as err:
            print(f'i: {i} r: {r}')
            raise err
        # print(f'i: {i} was found! the index: {r}')